Les 3 lois de Newton
Première loi de Newton :
Dans un référentiel
galiléen, le vecteur vitesse du centre d'inertie d'un système est constant
si et seulement si la somme des vecteurs forces qui s'exercent sur le système est un vecteur nul.
si et seulement si la somme des vecteurs forces qui s'exercent sur le système est un vecteur nul.
Deuxième loi de Newton :
Dans un référentiel galiléen, la somme vectorielle des forces
appliquées à un objet ponctuel est égale au produit de la masse de l’objet par
son vecteur accélération.
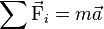
 : désigne
les forces extérieures exercées sur l'objet
: désigne
les forces extérieures exercées sur l'objet- m : la masse
 : l'accélération de
son centre d'inertie .
: l'accélération de
son centre d'inertie .
- · Cette loi permet l'étude quantitative du mouvement des corps .
- · on remarque aussi que si F = 0 alors a = 0 , on retrouve alors la première loi.
- · Cette loi est aussi appelé : théorème du centre d’inertie.
Troisième loi de Newton
:
Tout corps A exerçant une force sur un corps B
subit une force d'intensité égale, de même direction
mais de sens opposé,
exercée par le corps B.
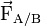 (exercée par A sur B) et la force
(exercée par A sur B) et la force  (exercée par B sur A) qui décrivent l'interaction sont directement opposées :
(exercée par B sur A) qui décrivent l'interaction sont directement opposées :




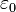 fois la charge électrique continue à l'intérieur de la surface fermé
fois la charge électrique continue à l'intérieur de la surface fermé






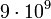 en unités
en unités 
















.jpg)